ドル・コスト平均法が最もよいか？

2009年02月01日に作成
タグ： FC2 投資 ☆☆☆

ドル・コスト平均法がいい理由としてよくあげられる例は 一定の株数を買うのと、一定の金額で買う場合を比べて 一定の金額で買うほうが平均単価が下がるからと説明されることが多い。

今回は、比べる対象を少し変えて本当にドル・コスト平均法が最もいいかを考えてみる。

例えば、宝くじや退職金など急にたくさんのお金が入ってきた場合、 一度に投資すべきか、少しずつ投資していくべきか迷うことがあると思う。

そこで、下の図のように６０万円の現金が手元にあり、１０年間投資する機会がある 場合を考えてみる。

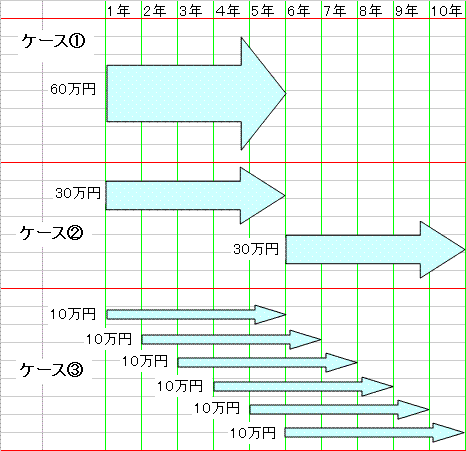
image

  • ケース①は1年目に60万を5年間投資して、6年目からは何もしない。
  • ケース②は1年目に30万を5年間投資して、6年目に30万を5年間投資する。
  • ケース③は1年目から6年目まで10万ずつ、すべて5年間投資する。

投資している金額×期間は同じなので期待値は同じであるはずである。 ケース①より、ケース②やケース③の方がばらつきが減りそうである。 だだ、ケース②とケース③がどっちがいいかは微妙なとこである。

そこで、投資の結果が対数正規分布に従うと仮定して、シミュレーションしてみた。 一年間の投資の結果は平均μ=1.05、標準偏差σ=0.2である対数正規分布とした。

＜シミュレーションの仕方＞

まず、それぞれ独立な対数正規分布（μ=1.05、σ=0.2）に従う乱数を10個 C1,C2,C3,…,C10 を生成させる。

  • ケース①の場合 60万×C1×C2×C3×C4×C5

  • ケース②の場合 30万×C1×C2×C3×C4×C5＋30万×C6×C7×C8×C9×C10

  • ケース③の場合 10万×C1×C2×C3×C4×C5＋10万×C2×C3×C4×C5×C6
    ＋10万×C3×C4×C5×C6×C7＋10万×C4×C5×C6×C7×C8
    ＋10万×C5×C6×C7×C8×C9＋10万×C6×C7×C8×C9×C10

を計算し、これを1000000回繰り返す。

この結果が下のグラフである。

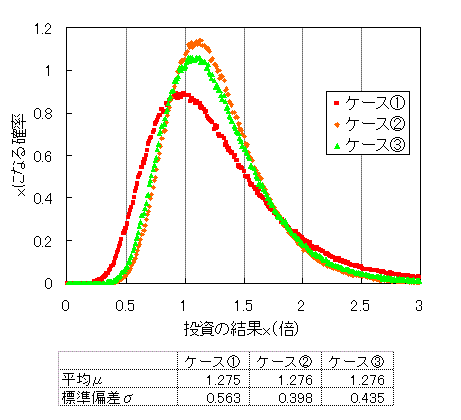
image

ケース①～③での乱数シミュレーション結果

平均は予想通りどのケースも同じで、約1.05^5=1.276倍になっている。 標準偏差はケース①より、ケース②・③の方が小さくなっている。 これは投資の結果が毎年独立で計算しているため、期間を分散することで、 分散効果が得られているからである。

ケース③の方がケース②よりもなんとなく標準偏差が小さいだろうと思っていた人もいると思う。 そこで下のようなケース②*を考えてみる。 ケース②と違い、はじめの5年と後の5年で金額を変えてある。 これも同様に乱数によるシミュレーションをしてμとσを出してある。

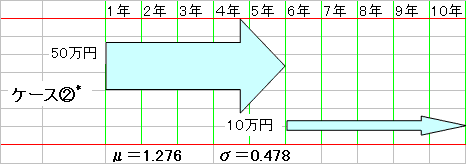
image

ケース②*のσはケース②よりも大きくなっている。 このことから、投資の金額が多い時期があるとσは大きくなると考えられる。 ケース③を見てみると、５・６年目など、投資の金額が多い時期がある。 このため、ケース②よりもσが大きくなったと考えられる。

今回の結論は、投資の結果が対数正規分布に従う（つまりランダムに動く）場合は、 ドルコスト平均法がベストとは限らないということである。

※2019年3月27日　 http://nukoriki.blog95.fc2.com/
より過去のブログのバックアップとして転記