７．対数正規分布を使ってみる

前回、対数正規分布は期間がn倍になると、 eの肩に乗っかっている正規分布のμeがn倍、σeが√n倍になることがわかった。 なので、今回実際に使ってみようと思う。 今まで乱数を使って計算していたけど、今回は式を使ってExcelで計算してみる。

まず、こちらのブログで使われていた TOPIXの、１年間の期待リターン4.80％、リスク22.15％を使って元本割れの確率を出してみる。 これより μ=1.048 σ=0.2215 となる。 今回はTOPIXが対数正規分布であると仮定する。 対数正規分布を考えるときは、eの肩に乗っかっている正規分布で考えたほうが考えやすい。 このため、これを、前に出てきた③、④式を使って、μe、σeに変換する。

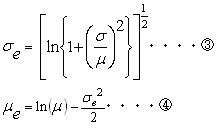
すると、 μe=0.0250 σe=0.2091 となる。 これは１年間の平均と標準偏差なので、ｎ年間の場合はμeをn倍、σeを√n倍にすればいい。 元本割れの確率はe^0=1よりも小さいとき、つまり、eの肩に乗っかる正規分布が0より 小さいときである。 このため元本割れの確率はExcelで　=NORMDIST(0,μe,σe,1)　を計算すればでてくる。

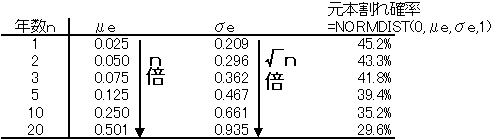
次にチューリップグラフというものをこちらのブログで見つけたので、対数正規分布で試してみる。 正規分布のμe±σeの間には68.3%の確率で入り、μe±２σeの間には95.4%の確率で 入ることは聞いたことがある人もいる思う。 ということで、とりあえずμe±σeとμe±２σeを計算する。

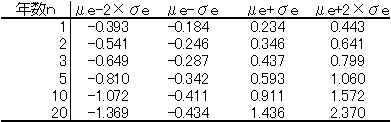
この値だとあまり意味がないので、これをeの肩に乗っけてやると、 例えば5年後の投資の結果が95.4%の確率で0.445倍～2.887倍の間になるとかがわかる。

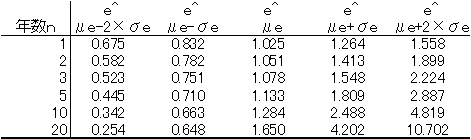
これをグラフにプロットしたのが下のグラフ。

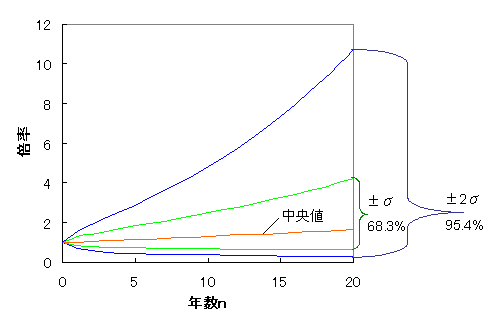
あんまり、チューリップの形になってない。かなり発散している。 20年後に元本を大きく下回る場合もありうることがわかる。

次に先ほどのブログでもう一つ試していた国内債券、国内株式、外国債券、外国株式 を同じ割合にしたポートフォリオ（リターンが4.08％、リスク9.61％）を 対数正規分布に従うと仮定して、同じことをしてみた結果が下のグラフである。

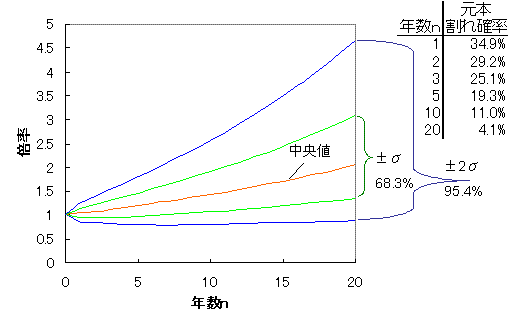
２０年後の元本割れの確率が少なくなり、見にくいけどマイナス側の線が 途中から上向きになっているのが見えると思う。 それでも、ちょっとチューリップの形というのは苦しい。

対数正規分布を使うと、どんどん発散していくので本当に現実とあっているのかは 疑問に思う部分がある。

※ここに書いたことは本とかでちゃんと調べたものでなく、正しいとは限らないので 　納得できたら使ってください。

※2019年3月27日　 http://nukoriki.blog95.fc2.com/
より過去のブログのバックアップとして転記