６．期間を考える（定率の場合）

前回、定額の投資をした場合を考えた。 期間がn倍になると、正規分布の標準偏差σが√n倍、平均μがn倍になるということだった。 今回は定率の場合を考えてみる。 定率の投資は対数正規分布になる（２回目と３回目）ということだった。 投資の期間をかえることを考えた場合、前の定額の場合と違い、今回は定率（現在持っている額 の内、一定の率で投資し続けること）なので、２年目の投資額は1年目の結果の額をそのまま投資 するのが正しいと思われる。

Xnをn年目は前の年に比べ何倍になったかを表すとし、 Xをn年間で合計何倍になったかを表すとすると、

X = X1 × X2 × X3 ×…× Xn　　（a)式 となる。

ここで、X1，X2，X3，…，Xnをそれぞれμ=1.02，σ=0.1の対数正規分布に従う乱数とし、 Xを計算するシュミレーションをしてみた。年数nは１年～１０年までそれぞれシミュレーションした。 サンプル数は1000000個。

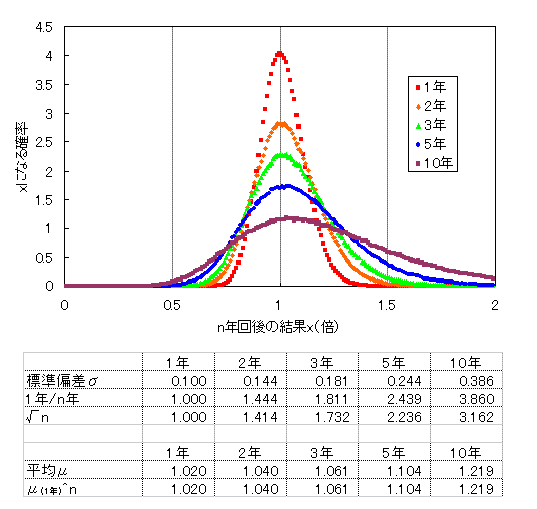　　　　　　対数正規分布（μ=1.02,σ=0.1）　１～10年のシミュレーション結果

正規分布の場合と違いσはｎ年後に√n倍にはなっていない。 また、μはn乗となっており、複利効果が出ている。

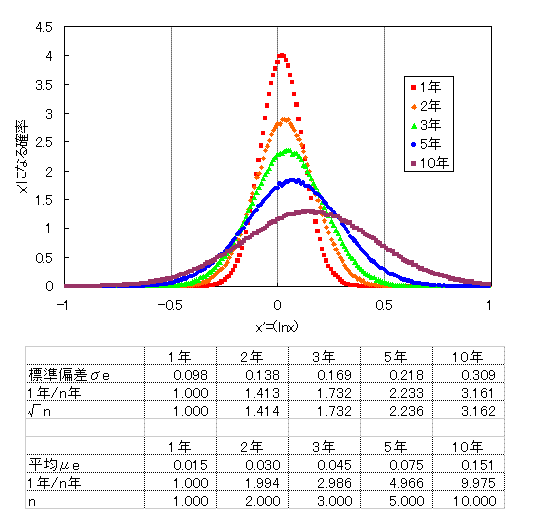
対数正規分布（μ=1.02,σ=0.1）の自然対数　１～10年のシミュレーション結果

対数正規分布の平均μと標準偏差σがn年後にどうなるかを式で考えてみる。

前々回出てきた①～④式の内、①、②式ににμe→ｎ×μe、σe→√ｎ×σeを代入すればいい。

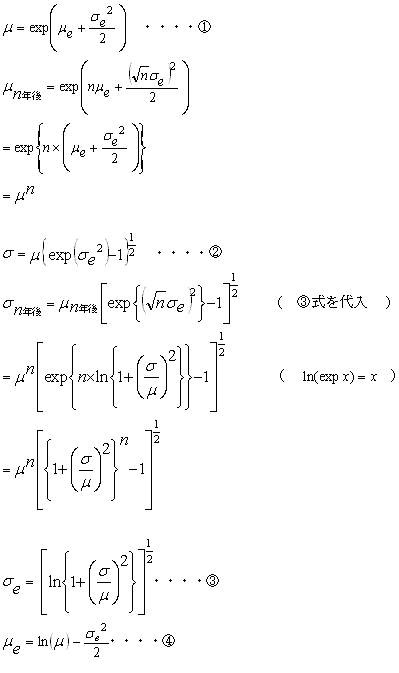
対数正規分布の平均μはn年後にｎ乗になることが式でもでてきた。 標準偏差σはちょっと複雑になってしまった。

これをまとめると下のようなイメージになる。

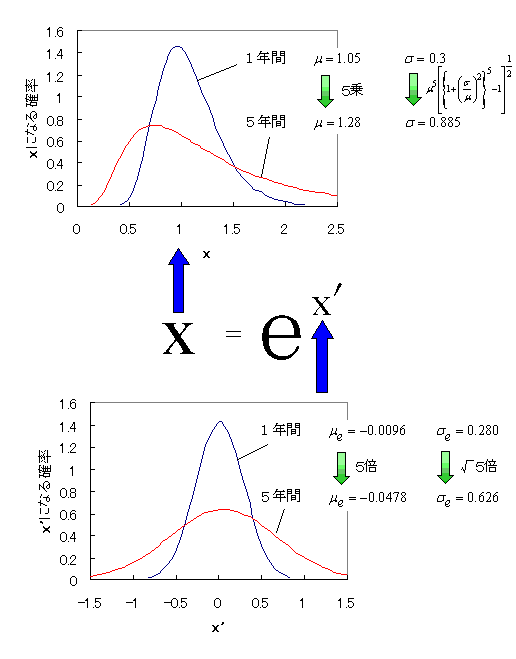
今回の結論は、対数正規分布は期間がn倍になると、 eの肩に乗っかっている正規分布のμeがｎ倍、σeが√n倍になるということである。

※2019年3月27日
http://nukoriki.blog95.fc2.com/ より過去のブログのバックアップとして転記