５．期間を考える（定額の場合）

前回までは、投資の期間について考えてこなかった。 今度は、投資の期間をかえると、どんな分布にかわっていくか考えてみたい。

２項分布の場合

まず、最初に戻って、定額で投資した場合で考えてみる。 はじめ100円を持っていて、0.1円賭け、1/2の確率で＋0.1円、1/2の確率で-0.1円になる 条件とする。 ここで、今回は賭けの回数を1万回～10万回とかえてやってみる。、 賭けにはある一定の時間がかかる場合、投資の期間をかえたとも解釈できる。 この乱数を使ってシミュレーションした結果が下のグラフである。サンプル数は1000000個。

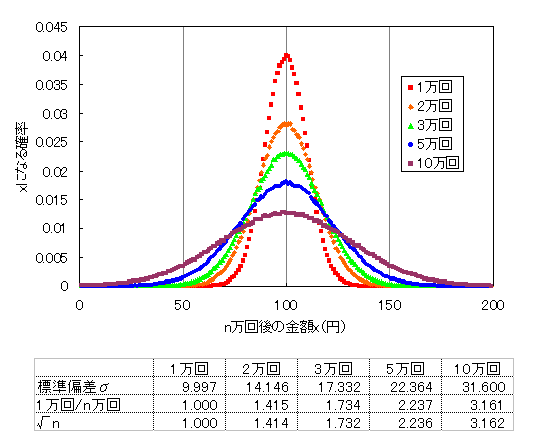
x=x+0.1 or x=x-0.1　１～10万回のシミュレーション結果

回数が増えるごとに分布は広がる。 また、標準偏差σは回数がn倍になると√n倍になっている。

正規分布の場合

これまでの結果より、定額の場合は正規分布に近づくということであった。 なので、正規分布で考えてみる。 最初１００円を持っており、１００円投資すると1年後にお金の増減量がμ=0,σ=10 の正規分布に従うような投資を考える。また、今回は定額の投資であるため、 2年目からも必ず１００円投資するとする。 もし、1年目で１００円以下になっても、誰かからお金を借りられるものと考えてみる。 そして、投資が終わった時に借りた分を返して、全部を合計するとする。

これを計算するときは下のように正規分布を足すことでできる。 n年後の金額　＝　100＋R1+R2+R3+…Rｎ （R1…Rｎはμ=0,σ=10の正規分布に従う乱数。)

投資期間を１～10年とし、正規分布に従う乱数を発生させてシミュレーションした結果が 下のグラフである。サンプル数は1000000個。

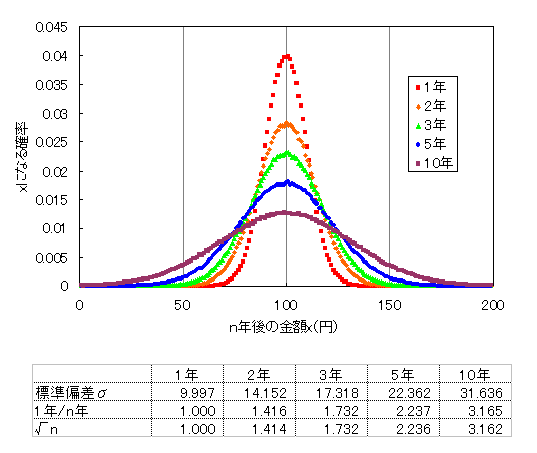
増減量が正規分布（μ=0,σ=10）　１～10年のシミュレーション結果

2項分布と同じように期間が増えるごとに分布は広がる。 また、標準偏差σは期間がn倍になると√n倍になっている。 もし、2年目からも１００円の定額ではなく、1年目に投資した結果の金額を そのまま投資した場合、このような分布にはならず、2項分布の結果と一致はしない。

次に、若干儲かる条件として1年後のお金の増減量をμ=2,σ=10にかえ、 同様に正規分布に従う乱数を発生させてシミュレーションした結果が下のグラフである。 サンプル数は1000000個。

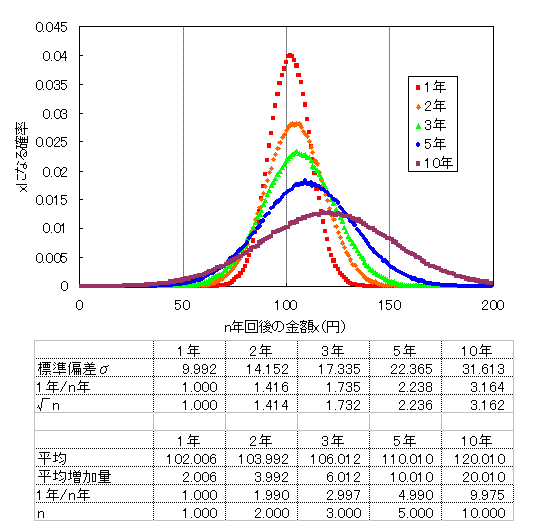
増減量が正規分布（μ=2,σ=10）　１～10年のシミュレーション結果

標準偏差σは期間がn倍になると√n倍になっているのは同じであり、 平均は期間がn倍になるとn倍増えている。 しかし、この場合複利効果はない。

これら結果より、正規分布をn回足した場合、 標準偏差σは√n倍となり、平均はn倍増える。

※2019年3月27日
http://nukoriki.blog95.fc2.com/
より過去のブログのバックアップとして転記