２．定率の投資の場合

前回は一定の金額をものすごく小さな金額ずつ投資した場合を考えてみた。 株式などは常に変動しており、投資額も常に変動していると考えることもできる。 そこで現在の金額に対し一定の率で投資した場合を考えてみる。

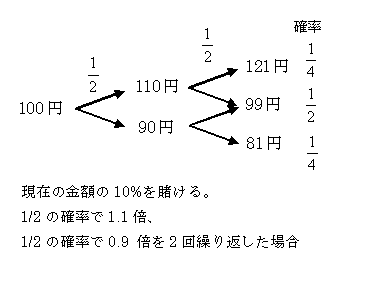
まずは簡単な例として、下図のように現在の10％の金額を賭けるとする。 現在110円の場合は11円賭けるということであり、 1/2の確率で1.1倍、1/2の確率で0.9倍になる。 前回の一定の金額の場合とは少しちがってくる。

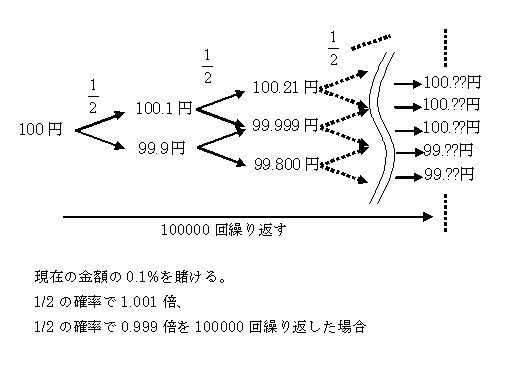
こんどは下図のように1回あたりの掛け金を0.1%にして、100000回続けた場合を 乱数を使ってシミュレーションしてみた。サンプル数は1000000個。

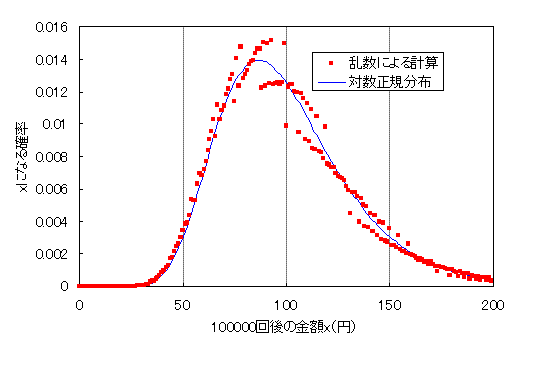
x=x+0.1 or x=x-0.1、100000回のシミュレーション結果

乱数シミュレーション結果は平均μ=99.989、標準偏差σ=32.442。 この平均と標準偏差を使った対数正規分布がグラフに重ねてある。 対数正規分布に関してはあとで、詳しく説明するつもりなので、気にしないでください。

若干よくわからない分布が出てきたので、ここで自然対数をとってみる。 はじめの金額（ここでは100円）と、100000回後の金額ｘの比に自然対数をとった、 x’=ln(x/100)　を横軸にしてグラフにしたのが下の図である。

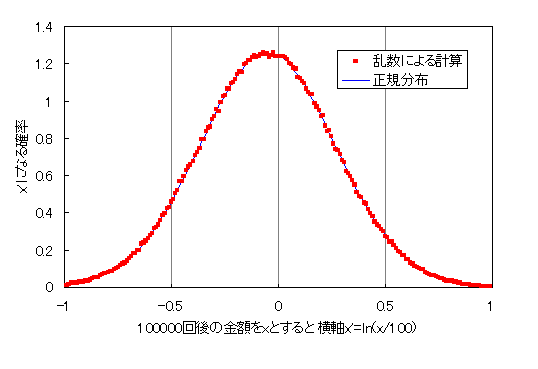
x=x+0.1 or x=x-0.1、100000回のシミュレーション結果 　（横軸をx’=ln(x/100)にしたもの）

x’の平均μe=-0.0502、標準偏差σe=0.3164。

自然対数をとると正規分布になっている。

この理由について考えてみた。 100000回のうち勝負に勝った回数をn回、負けた回数をm回（m=100000-n)とすると x’＝ln(1.001^n×0.999^m)
＝m×ln(1.001) ＋ n×ln(0.999)
＝m×0.9995 ＋ n×(-1.0005) となる。

つまり、前回の自然対数をとったものの分布は 勝ったらプラス0.9995円、負けたらマイナス1.005円の賭けを100000回したものと同じになる。

前回、勝った時の報酬を少し増やしたものでも正規分布になったので、 （今回は負けたほうの損が大きいが、勝ちと負けの報酬が同じなくても 正規分布になるという意味で）、当然、今回も正規分布になったのである。

今回の結論は定率の小さなの賭けを繰り返すと、 結果の自然対数をとったものが正規分布になるということである。

※2019年3月27日
http://nukoriki.blog95.fc2.com/
より過去のブログのバックアップとして転記